Complejidad de un algoritmo (notación Big-O)
La complejidad de un algoritmo nos permite entender cómo se va a comportar el algoritmo cuando incrementemos la cantidad de datos de entrada.
Por ejemplo, en un algoritmo que ordena una lista, la complejidad nos va a permitir saber cómo se va a comportar ese algoritmo cuando tenga 100,000 o 1 millón de elementos.
Notación Big-O
La complejidad del algoritmo es independiente de la velocidad del computador en el que se ejecuta y se define utilizando la notación Big-O. La idea es conocer cuántas operaciones se necesitan a medida que aumentan los datos de entrada.
Complejidad lineal - O(n)
A medida que aumentan los datos el número de operaciones aumenta de forma proporcional. Por ejemplo, si necesitamos 1 operaciones por cada dato, vamos a necesitar 10 operaciones para 10 datos y 100 operaciones para 100 datos.
La siguiente gráfica muestra la relación entre el número de datos (eje x) y el número de operaciones (eje y):
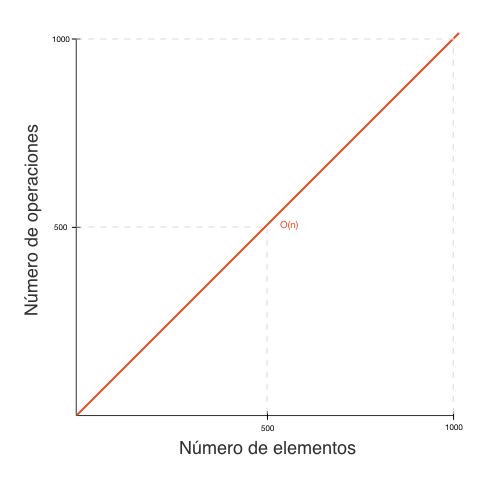
El ejemplo del capítulo anterior en el que describimos una búsqueda simple en un arreglo es un ejemplo de una complejidad lineal O(n).
También puede ocurrir que recibamos dos listas como datos de entrada y debamos recorrerlas de forma independiente. En este caso la complejidad sería O(n+m) donde n es la longitud de la primera lista y m la longitud de la segunda lista.
Complejidad exponencial - O(n^2), O(n^3), etc.
A medida que aumenta la cantidad de datos, el número de operaciones crece de forma exponencial. Por ejemplo, una complejidad cuadrática (O(n^2)) si para un dato necesitamos 2 operaciones, para 2 datos vamos a necesitar 4 operaciones, para 3 datos 9 operaciones y así sucesivamente.
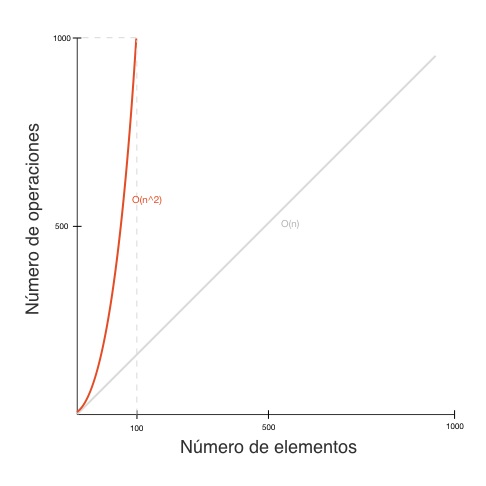
En la vida real la complejidad exponencial ocurre cuando tenemos ciclos anidados. Dos ciclos anidados generan una complejidad O(n^2), tres ciclos anidados O(n^3) y así sucesivamente.
También puede ocurrir que recibamos dos listas que debamos recorrer de forma anidada. En este caso la complejidad sería O(n*m) donde n es la longitud de la primera lista y m la longitud de la segunda lista.
Nota: No confundir O(n*m) que es exponencial con O(n+m) que es lineal.
Complejidad logarítmica O(log n)
A medida que aumenta la cantidad de datos, el número de operaciones aumenta, pero no de forma proporcional a los datos.
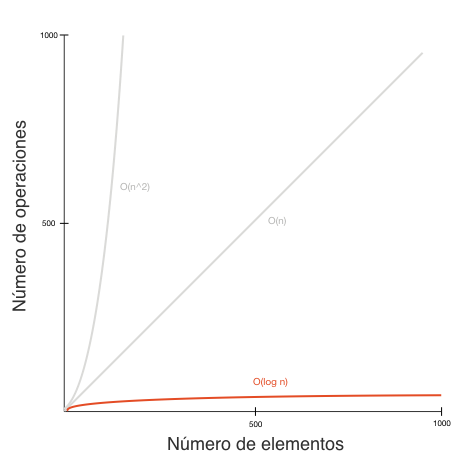
En la vida real la complejidad logarítmica se da en casos en los que no es necesario recorrer todos los elementos. Por ejemplo, para adivinar un número de 1 a 100 podemos intentar con 50 y preguntar si el número es mayor o menor. Si es mayor intentamos con 75 y repetimos el proceso acercándonos cada vez más a la respuesta.
Complejidad constante - O(1)
A medida que aumenta la cantidad de datos el número de operaciones se mantiene constante.
O(1) significa que sólo se ejecuta una operación, O(2) significa que se ejecutan dos operaciones, O(3) tres operaciones y así sucesivamente. Pero el número de operaciones no es importante, lo importante es que, independiente del número de datos de entrada, el rendimiento va a ser constante.
Una operación puede ser una asignación de una variable, una comparación, o algún cálculo aritmético (suma, resta, multiplicación, división, etc.), entre otros.
Escenarios (peor, mejor y promedio)
Cuando se habla de la notación Big-O nos podemos referir al peor, mejor o al escenario promedio. Por ejemplo, en el algoritmo de búsqueda del capítulo anterior que nos permite encontrar un elemento en una lista:
- El peor escenario asume que el elemento se va a encontrar en la última posición.
- El mejor escenario asume que el elemento se va a encontrar en la primera posición.
- El escenario promedio asume que el elemento se va a encontrar en la mitad de la búsqueda.
Aunque existen notaciones para expresar el mejor escenario y el escenario promedio, es más conservador, común y fácil referirse al peor escenario cuando se habla de complejidad de un algoritmo como lo hemos hecho en este capítulo.
Complejidad espacial
La complejidad espacial es la cantidad de memoria que requiere el algoritmo. Algunas veces es posible reducir la complejidad temporal incrementando la complejidad espacial y viceversa.
Por ejemplo, un algoritmo que utiliza una variable adicional es O(1). Un algoritmo que utiliza una lista adicional es O(n).